840 05 Bratislava 45
tel.: +421 2 50 236 222

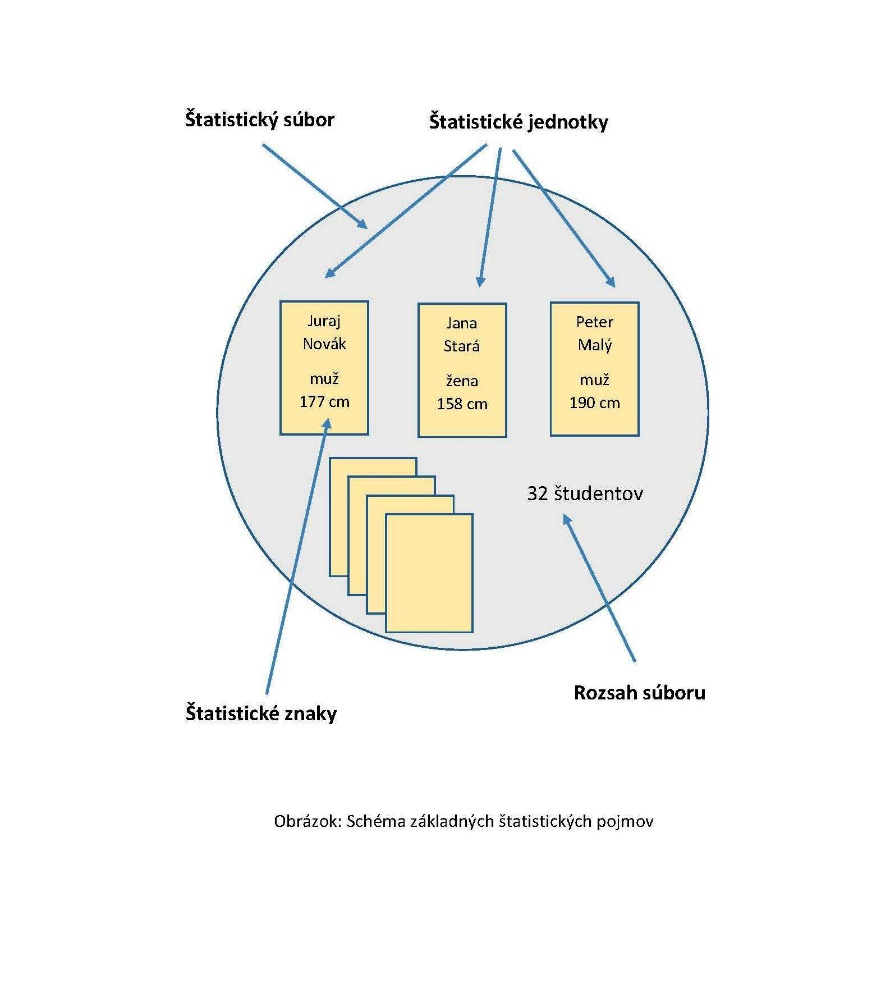
Pre jednoduchšie pochopenie štatistiky je potrebné vysvetliť niektoré základné štatistické pojmy.
Štatistika sa zaoberá javmi, ktoré nazývame hromadné javy. Rozlišujeme dva druhy hromadných javov. Jeden druh je taký, čo sa vyskytuje vo veľkom počte objektov - výška, hmotnosť, farba očí, pohlavie, vek, profesia, počet detí a pod. Druhý druh je taký, ktorý je výsledkom veľkého počtu opakovaní, napr. opakované váženie nejekého predmetu, opakované hody kockou, mincou a pod. Objekty, ktoré skúma štatistika voláme štatistický súbor - napr. množina osôb, ktoré žijú na nejakom území.
Základný štatistický súbor rozsahu N predstavuje množinu všetkých štatistických jednotiek. V prípade, že nemožno skúmať základný súbor (z časových, finančných alebo iných dôvodov), vytvárame z neho výberový súbor podľa vopred stanovených pravidiel. V prieskume sa údaje zbierajú len za časť populácie, tzv. vzorku. Tieto údaje sa potom použijú na odhad charakteristík celej populácie. V tomto prípade sa musí zabezpečiť, aby vzorka reprezentovala príslušnú populáciu. Napríklad podiel osôb vo veku do 18 rokov alebo podiel žien a mužov vo vybranej vzorke domácností musí odrážať realitu v celkovom počte obyvateľov.
Výber musíme urobiť tak, aby vybrané objekty mali vlastnosť, ktorú má aj celý základný súbor. Túto vlastnosť nazývame štatistický znak (môže to byť pohlavie, profesia, počet detí, vek, vzdelanie a pod.). Rôzne hodnoty štatistického znaku voláme obmeny, varianty.
Štatistické znaky možno deliť podľa rôznych hľadísk. Základné delenie je na znaky kvalitatívne a kvantitatívne:
Kvalitatívne (kategoriálne) znaky slovne vyjadrujú vlastnosť štatistickej jednotky. Hodnoty kvalitatívnych znakov sa zvyknú označovať číslami, okódujú sa. Kvalitatívne znaky delíme na:
Kvantitatívne (kardinálne, číselné) znaky sú reálne čísla, môžeme o ich hodnotách povedať, či sú rovnaké alebo rôzne, vieme ich usporiadať do poradia a vieme tiež určiť, o koľko je jedna hodnota väčšia ako druhá. Tieto znaky majú aj nulovú hodnotu a meraciu jednotku. Kvantitatívne znaky delíme na:
Intervalové znaky (rozdielové) sú tie, ktorých hodnoty môžeme usporiadať do poradia, vieme určiť, o koľko je jedna hodnota väčšia ako druhá a aké sú rozdiely (intervaly) medzi hodnotami, ale nevieme určiť, koľkokrát je jedna hodnota väčšia ako druhá. Intervalový znak nemá prirodzený nulový bod, ale nulový bod možno určiť dohodou. Preto sa hodnoty intervalového znaku môžu sčitovať alebo odčitovať, ale nemôžu sa násobiť a deliť. Môžu nadobúdať kladné aj záporné hodnoty, napríklad: znak „Celziova teplota“ má dohodnutú nulu – teplotu topenia ľadu.
Pomerové znaky (podielové) sú špeciálne prípady intervalových znakov. Možno ich usporiadať do poradia a vieme určiť rozdiely medzi hodnotami. Majú tiež prirodzený nulový bod, absolútnu 0, ktorá znamená, že znak neexistuje. Ich hodnoty nemôžu byť záporné, možno ich sčitovať, odčitovať, násobiť aj deliť. Napríklad znak vek má absolútnu nulu 0 rokov. 60 ročný človek má o 40 rokov viac ako 20 ročný a pritom môžeme povedať, že je 3 krát starší ako dvadsiatnik.
Zisťovanie hodnôt štatistického znaku v štatistickom súbore sa volá štatistické zisťovanie. Pri štatistickom spracovávaní údajov často nahrádzame kvalitatívny znak kvantitatívnym.
(napríklad kvalitatívny znak pohlavie: muži = 1, ženy = 2).
Znak, ktorý má iba jednu nemennú hodnotu sa volá konštanta. V štatistike sa sledujú hlavne znaky, ktoré majú aspoň dve alebo viac obmien. Takýto znak má názov premenná.
Údaje získané štatistickým zisťovaním najlepšie zjednodušíme a sprehľadníme tým, že ich usporiadame do určitých skupín – tried.
Metóda usporiadania štatistických údajov do určitých skupín (tried) podľa určitého znaku sa nazýva triedenie.
triedenie = rozdelenie štatistických jednotiek do takých skupín (tried), aby čo najlepšie vynikli charakteristické vlastnosti skúmaných javov;
triediaci znak = štatistický znak, ktorý je kritériom triedenia štatistického súboru;
trieda = skupina štatistických jednotiek s rovnakou hodnotou (variantom) znaku.

Príklady triedenia štatistických súborov:
- pri známkovaní v škole rozlišujeme triedu jednotiek, triedu dvojok, trieda trojok, ...
- triedenie osôb podľa dosiahnutej úrovne vzdelania - skupina so základným vzdelaním, skupina so stredným vzdelaním, bez maturity, skupina so stredným vzdelaním s maturitou.
Keď má štatistický znak malý počet obmien, tak každá jeho obmena predstavuje samostatnú triedu. Na prezentáciu takýchto údajov sa používa tabuľka rozdelenia početností, ktorá sa tiež volá frekvenčná tabuľka. Obvykle ide o prvý krok pri spracovaní štatistických údajov.
Tabuľky početnosti slúžia na zobrazenie údajov, je to prehľadný spôsob usporiadania údajov. Štatistické údaje sa zaraďujú do tried s určitým počtom a vytvorí sa rozdelenie početnosti.
Tabuľky početnosti obsahujú informácie:
Príklad
V domácnostiach sa zisťoval počet obytných miestností s možnými výsledkami: 1, 2, 3, 4, 5+ (znamená 5 a viac miestností). Pri tomto zisťovaní bolo náhodne vybratých 25 respondentov s nasledujúcimi výsledkami, ktorí žili v bytoch s nasledovným počtom miestností: 1, 3, 2, 4, 5+, 2, 3, 2, 5+, 1, 4, 2, 3, 3, 5+, 3, 3, 2, 4, 4, 2, 3, 4, 3, 2
Vytvorte tabuľku rozdelenia početností a relatívnych početností. Pokúste sa o stručnú interpretáciu získaných výsledkov, ktorá bude obsahovať najpočetnejšiu a najmenej početnú hodnotu sledovaného znaku.
Riešenie
Sledovaný znak označíme symbolom x (počet obytných miestností), ktorý môže nadobudnúť hodnoty xi (j = 1, 2, 3, 4, 5+). Absolútne početnosti označíme ni, relatívne početnosti vj.
Tabuľka: Absolútne a relatívne početnosti podľa počtu obytných miestností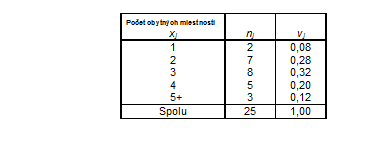
Najviac osôb žije v domácnostiach s troma obytnými miestnosťami (32 %), kým domácnostiach s jednou obytnou miestnosťou žije najmenej osôb (8 %).
Poznáme dve základné skupiny číselných charakteristík pre skúmanie jedného štatistického znaku:
charakteristiky polohy (stredu) - vyjadrujú určitú úroveň znaku, okolo ktorej sú ostatné hodnoty znaku viac alebo menej koncentrované;
charakteristiky variability (premenlivosti) - vyjadrujú, ako sa hodnoty znaku prvkov súboru líšia od zvolenej charakteristiky polohy, respektíve od seba navzájom
Charakteristiky polohy (úrovne, stredu) - čísla, ktoré určitým spôsobom charakterizujú tzv. "priemernú hodnotu" sledovaného štatistického znaku. Delíme ich na dve základné skupiny:
- priemery - môžu byť jednoduché alebo vážené
a) aritmetický priemer
b) geometrický priemer
c) harmonický priemer
- ostatné stredné hodnoty - medián, modus
Aritmetický priemer, v bežnom jazyku sa nazýva priemer, je súčtom hodnôt skupiny čísel vydelených počtom čísel v skupine. Priemer možno chápať ako zhrnutie skupiny čísel do jedného čísla.
Aritmetický priemer x̄ vyjadruje, aký objem hodnôt znaku X pripadá v priemere na jednu jednotku súboru. Je definovaný vzťahom:
![]()
N - rozsah súboru,
xi - hodnota znaku X u i-tej jednotky.
Príklad
Máme 9 čísel v skupine: 10, 12, 11, 15, 13, 35, 41, 23, 20. Súčet týchto 9 čísel je 180. Potom sa suma 180 delí číslom 9, aby sa dosiahol priemer. Priemer je 180/9 = 20.
Príklad
Na základe štatistických hlásení o narodeniach a úmrtiach a súboroch o sťahovaní spracúva Štatistický úrad SR každoročnú bilanciu počtu obyvateľov Slovenskej republiky za všetky obce.
K dispozícii máme stredný (priemerný) počet trvale bývajúceho obyvateľstva v jednotlivých krajoch SR k 31. 12. 2018 (pre lepšiu prácu s údajmi bol počet obyvateľov zaokrúhlený a uvádza sa v tisícoch): Bratislavský kraj 646, Trnavský kraj 562, Trenčiansky kraj 588, Nitriansky kraj 679, Žilinský kraj 691, Banskobystrický kraj 650, Prešovský kraj 823, Košický kraj 798.
Vypočítajte aritmetický priemer počtu obyvateľov žijúcich v jednom kraji Slovenskej republiky.
Riešenie
Uvedené údaje dosadíme do vzorca pre aritmetický priemer. Nesmieme zabudnúť, že do vzorca budeme dosadzovať čísla uvedené v tisícoch, preto aj výsledný počet obyvateľov bude v tisícoch.
x̄ = (646+562+588+679+691+650+823+798)/8 = 679,625 ≐ (približne) 680
Môžeme konštatovať, že v každom kraji Slovenskej republiky žije v priemere 680 tisíc obyvateľov.
Aritmetický priemer (ilustračné video môže obsahovať reklamy)
V oficiálnych štatistikách je najčastejším typom priemeru vážený priemer, pretože málokedy majú všetky položky rovnaký význam. Vo váženom priemere sa každá položka, ktorá sa berie do úvahy, vynásobí číslom (váhou), ktoré odráža relatívny význam položky, potom sa výsledok spočíta a následne sa vydelí počtom položiek.
Vážený aritmetický priemer x̄ používame, ak pracujeme s triedeným súborom hodnôt znaku X. Na jeho výpočet použijeme vzťah :
![]()
N - rozsah súboru,
xi - hodnota znaku X u i-tej jednotky.
Vážený priemer (ilustračné video v češtine môže obsahovať reklamy)
Geometrický priemer (ilustračné video môže obsahovať reklamy)
Mo je najčastejšie sa vyskytujúca hodnota znaku X, resp., v prípade triedeného súboru hodnota s najväčšou absolútnou početnosťou.
PríkladMedián Me je hodnota, ktorá súbor zistených hodnôt delí na 2 rovnako početné skupiny, t. j. skupiny, z ktorých prvá obsahuje 50 % štatistických jednotiek, ktoré majú hodnotu znaku X menšiu ako medián, druhá obsahuje 50 % zvyšných štatistických jednotiek, ktoré majú hodnotu väčšiu ako medián. Ak zoradíme všetky hodnoty znaku podľa veľkosti do neklesajúcej (resp. nerastúcej) postupnosti, tak mediánom bude hodnota, ktorá je v strede uvažovanej postupnosti.
Me = xk+1, ak N = 2k + 1,
M
e = (xk + xk+1)/2, ak N = 2k
V prípade triedeného súboru:
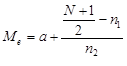
a - horná hranica triedy, ktorá predchádza mediálny interval,
N - rozsah súboru,
n1 - počet všetkých prvkov pod mediálnym intervalom,
n2 - počet prvkov mediálneho intervalu,
h - šírka triedy.
Riešenie
a) Najprv si vypočítame povrchy (v cm2) jednotlivých kociek. Pre dané rozmery hrán sa postupne rovnajú: 216, 384, 486, 600, 726.
Teraz je možné určiť medián:
Med (x) = x(n+1)/2 = x6/2
= x3 = 486, pretože n je nepárne.
Modus, medián (ilustračné video môže obsahovať reklamy)
Charakteristiky variability (premenlivosti,
rozptýlenia) = čísla, ktoré udávajú, do akej miery sa hodnoty znaku odchyľujú od zvolenej charakteristicky polohy, respektíve od seba navzájom. Patria k nim:
- variačné rozpätie
- rozptyl
- smerodajná odchýlka
Variačné rozpätie vr je iba približnou charakteristikou variability hodnôt sledovaného znaku. Je definovaný ako rozdiel najväčšej a najmenšej hodnoty kvantitatívneho znaku, t. j. v r = xmax - xmin .
Rozptyl δ2 predstavuje aritmetický priemer druhých mocnín (štvorcov) odchýlok od priemeru x̄. Je definovaný vzorcom:
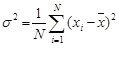
V prípade triedeného súboru ho vypočítame podľa vzťahu:
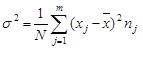
N - rozsah súboru,
m - počet tried v súbore,
nj - absolútna početnosť j-tej triedy (j = 1, 2, ...,
m),
xj - hodnota znaku X, ktorá reprezentuje j-tu triedu.
K dôležitým vlastnostiam rozptylu patrí:
a) Rozptyl konštanty je rovný nule.
b) Ak pripočítame ku všetkým hodnotám znaku konštantu, rozptyl sa nezmení.
c) Ak všetky hodnoty znaku vynásobíme konštantou a , potom rozptyl takto vzniknutých hodnôt je rovný súčinu rozptylu pôvodného súboru a druhej mocniny konštanty a .
Príklad
V predajni hospodárskych potrieb dostali zásielku 18 metiel, pričom metly mali mať predpísanú dĺžku 120 cm. Meraním sa však zistilo, že skutočné dĺžky sú nasledujúce:
117, 122, 125, 118, 119, 120, 122, 123, 116, 117, 121, 120, 123, 120, 119, 121, 124, 115.
Určite rozptyl metiel.
Riešenie
Najskôr vypočítame priemer:
x̄ = (117+122+125+118+...+121+124+115) / 18 = 2162 / 18 = 120,1
Dosadením do vzorca vypočítame rozptyl:

Výsledný rozptyl sa rovná 6,69.
Rozptyl (ilustračné video môže obsahovať reklamy)
Úvod do rozptylu a smerodajnej odchýlky (ilustračné video môže obsahovať reklamy)
Štandardná (smerodajná) odchýlka δ je definovaná ako δ=√δ2 a udáva, ako sa v priemere v danom súbore odchyľujú hodnoty znaku od aritmetického priemeru.
Smerodajná odchýlka (ilustračné video môže obsahovať reklamy)